目錄
求和法 Summation of arithmetic sequence
求和法 Summation of geometric sequence
無論想補底,想清Concept,定係aim 5**,可以 <<查看更多>> 。
等差數列 Arithmetic sequence (AS)
首先要知道最基本的符號/公式!
Tn = 第n項 nth term/ 數列中的通項 General term
a = 首項 First term
d = 公差 Common difference
(** d的數字必須是後項減前項! **)
T1 = a, T2 = a + d, T3 = a + 2d, T4 = a + 3d, T5 = a + 4d, 如此類推
(** a 和 d 可以是正數或負數 **)
數列的通項 general term
Tn = a + (n-1) d
以2020 P2 Q35為例,練習一下找 d!
| Question |
If a > 0, which of the following are arithmetic sequences? I. log a-3, log a, log a5 II. 8-4a, 9-5a, 10-6a III. cos(90-a)°, cos90°, cos(90+a)° |
| Option |
a. I and II only b. I and III only c. II and III only d. I, II and III |
不要偷看答案喔!做完再往下看答案~ Solution

Solution
|
For I, log a – log a-3 = log a – (-3) log a =4 log a Log a5 – log a = 5 log a – log a = 4 log a Both d = 4 log a, so I is AS. |
|
For II, (9 – 5a) – (8 – 4a) = 9 – 5a – 8 + 4a = 1 – a (10 – 6a) – (9 – 5a) =10 – 6a – 9 + 5a = 1 – a Both d = 1 – a, so II is AS. |
|
For III, cos 90° – cos (90 – a)° = 0 – sin a° = – sin a° cos (90 + a)° – cos 90° = – sin a° – 0 = – sin a° Both d = – sin a°, so III s AS. ANS = D (I, II and III) |
再來一條練習題目!2018 P2 Q12
| Question |
Let an be the n th term of a sequence. If a3 = 21, a6 = 89 and a n+2 = an + a n+1 for any positive integer n, then a1 = |
| Option |
a. 8 b. 13 c. 34 d. 55 |
Solution
|
a6 = a4+2 89 = a4 + a5 89 = a4 + a4 + a3 89 = 2a4 + 21 a4 = 34 |
|
a4 = a2 + a3 32 = a2 + 21 a2 = 13 a3 = a1 + a2 21 = a1 + 13 a1 = 8 ANS = A (8) |
**當然面對MC題目, 只要sub answer就可以快速解決!
無論想補底,想清Concept,定係aim 5**,可以 <<查看更多>> 。
求和法 Summation of arithmetic sequence
Sn = 首n項的總和Sum
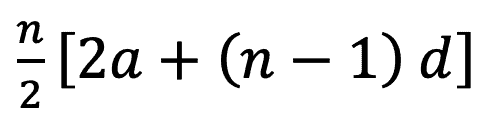
看看2019 P1 Q16b,AS有時候會和其他課題一起出題。

因為重點想讓同學們練習AS,所以先提供 (a)的答案! 分別是 9 和 27。

The least value of n is 60.

搞清AS後,繼續看下去,看看GS的公式~
等比數列 Geometric sequence
首先要知道最基本的符號/公式!
等比數列基本功
a = 首項 First term
r = 公比 Common ratio
(** r的數字必須是後項除前項! **)
T1 = ar, T2 = ar1, T3 = ar2, T4 = ar3, T5 = ar4, 如此類推
等比數列通項 General form
Tn = arn-1
求和法 Summation of geometric sequences
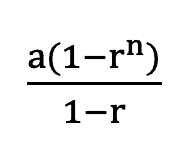
無限項之和公式 Sum to infinity

試試2016 P2 Q36


Solution

再來一條2020年的Paper 1 題目 Q16


考評局第五級示例
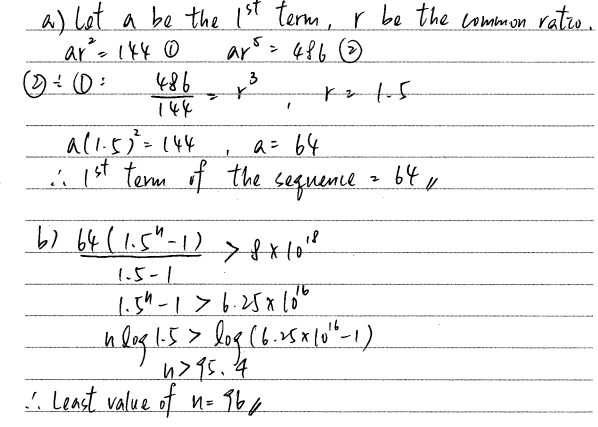


無論想補底,想清Concept,定係aim 5**,可以 <<查看更多>> 。
AS GS 計算機 Program
有興趣加AS GS 的計算機program,可以點點這裡 ->>>>> ASGS-Program
對於計算時或check數時會有幫助!
總結
其實ASGS不只會單獨出題,有時還會跨課題出題,例如Inequalities不等式, Probabilities概率, Compound interest複利息,而且每年Paper1和2必定有ASGS的題目,所以必須要搞清楚ASGS的公式和怎麼運用!這裡沒有講太多關於跨課題的題目例子,先學好基本的東西~
無論想補底,想清Concept,定係aim 5**,可以 <<查看更多>> 。
有興趣想了解geometric sequences怎樣套用在investment投資的題目上,就可以看看以下例子!看似複雜,掌握後便覺得沒想像中那麼難~


















